دفترچه راهنما:
راهنمای برنامه تسطیح به همراه کلیه جزئیات و دفترچه محاسبات تکمیل و راه اندازی شد،ایجاد شبکه منظم:
نقشه های توپوگرافی حاوی رقوم ارتفاعی زمین طبیعی در رئوس شبکه هاي منظم و همچنین رقوم ارتفاعی پراکنده و یا نامنظم می باشند که برنامه تسطیح از این رقوم به منظور مبنای محاسبات خود استفاده می کند. نسخه جدید برنامه تسطیح به منظور کنترل دقیق تر و استفاده بهینه از این رقوم در مرحله ابتدایی اقدام به ساخت یک فایل شبکه بندی شده منظم یا Grid فایل می نماید که می توان تا پایان پروژه از آن به عنوان فایل ورودی رقوم ارتفاعی زمین استفاده کرد.
هدف از شبکه بندی رسیدن از یک مجموعه نامنظم نقاط به یک مجموعه منظم است که در عملیات تسطیح کاربرد دارد.
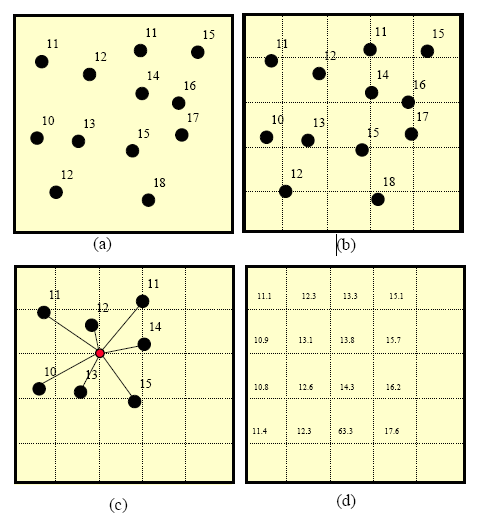
تصویر بالا شمای ساده ای از ایجاد یک شبکه منظم از مجموعه ای از نقاط را در چهار مرحله نمایش می دهد.
شکل c – محاسیه رقوم رئوس شبکه را نشان می دهد
روشهای واسطه یابی:
نسخه جدید برنامه جهت ایجاد فایل شبکه منظم رقوم ارتفاعی ( گرید فایل ) از روشهای زیر استفاده کند.The Inverse Distance to a Power method The Inverse Distance to a Power method is a
weighted average interpolator, which can be either exact or smoothing. With
Inverse Distance to a Power, data are weighted during interpolation, so that
the influence of one point, relative to another, declines with distance from
the grid node. Weighting is assigned to data through the use of a weighting
power, which controls how the weighting factors drop off as distance from the
grid node increases. The greater the weighting power, the less effect the
points, far removed from the grid node, have during interpolation. As the
power increases, the grid node value approaches the value of the nearest
point. For a smaller power, the weights are more evenly distributed among the
neighboring data points. Normally, Inverse Distance to a Power behaves as an
exact interpolator. When calculating a grid node, the weights assigned to the
data points are fractions, the sum of all the weights being equal to 1.0.
When a particular observation is coincident with a grid node, the distance
between that observation and the grid node is 0.0, that
observation is given a weight of 1.0; all other observations are given
weights of 0.0. Thus, the grid node is assigned the value of the coincident
observation. The smoothing parameter is a
mechanism for buffering this behavior. When you assign a non-zero
smoothing parameter, no point is given an overwhelming weight, meaning that
no point is given a weighting factor equal to 1.0. One of the characteristics
of Inverse Distance to a Power is the generation of "bull's-eyes"
surrounding the observation position within the grid area. A smoothing
parameter can be assigned during Inverse Distance to a Power to reduce the
"bull's-eye" effect by smoothing the interpolated grid
Inverse Distance to a Power در اين روش واسطه يابي بوسيله ميانگين
وزني داده ها انجام ميشود
يعني تاثير نسبي يك نقطه با دور شدن از شبكه كاهش مي
يابد |
|
The Kriging Method
Kriging is a geostatistical gridding method that has proven useful and popular in many fields. This method produces visually appealing maps from irregularly spaced data. Kriging attempts to express trends suggested in your data, so that, for example, high points might be connected along a ridge rather than isolated by bull's-eye type contours. Kriging is a very flexible gridding method. The Kriging defaults can be accepted to produce an accurate grid of your data, or Kriging can be custom-fit to a data set, by specifying the appropriate variogram model. Within SURFER, Kriging can be either an exact or a smoothing interpolator, depending on the user-specified parameters. It incorporates anisotropy and underlying trends in an efficient and natural manner.  Kriging اين روش که روش پيش فرض نرم افزار می باشد جزو قابل اطمينان ترين گزينه ها بين روش هاي واسطه يابي است و در بسياري از زمينه ها كاربرد دارد |
|
The Minimum Curvature Method Minimum Curvature is widely used in the
earth sciences. The interpolated surface generated by Minimum Curvature is
analogous to a thin, linearly elastic plate passing through each of the data
values, with a minimum amount of bending. Minimum Curvature generates the
smoothest possible surface while attempting to honor your data as closely as
possible. Minimum Curvature is not an exact interpolator, however. This means
that your data are not always honored exactly
 Minimum Curvature روش كمترين انحنا بطور گسترده در علم زمين
شناسي استفاده ميشود.سطحي كه با اين
روش ساخته ميشود شبيه يک صفحه نازك كشسان است كه با انحناي كم از داده ها مي گذرد. |
|
The Modified Shepard's Method
The Modified Shepard's
Method uses an inverse distance weighted least squares method. As such,
Modified Shepard's Method is similar to the Inverse Distance to a Power
interpolator, but the use of local least squares eliminates or reduces the
"bull's-eye" appearance of the generated contours. Modified
Shepard's Method can be either an exact or a smoothing interpolator. The
Surfer algorithm implements Franke and Nielson's (1980) Modified Quadratic
Shepard's Method with a full sector search as described in Renka (1988).
Modified Shepard's Method اين روش شبيه به روش Inverse Distance to a Power است با اين تفاوت كه معادلات كمترين مربعات حل شده، به صورت محلي است. |
The Natural Neighbor Method
The Natural Neighbor method is quite
popular in some fields. What is the Natural Neighbor interpolation? Consider
a set of Thiessen polygons (the dual of a Delaunay triangulation). If a new
point (target) were added to the data set, these Thiessen polygons would be
modified. In fact, some of the polygons would shrink in size, while none
would increase in size. The area associated with the target's Thiessen
polygon that was taken from an existing polygon is called the "borrowed
area." The Natural Neighbor interpolation algorithm uses a weighted
average of the neighboring observations, where the weights are proportional
to the "borrowed area". The Natural Neighbor method does not
extrapolate contours beyond the convex hull of the data locations (i.e. the
outline of the Thiessen polygons).
Natural Neighbor اين روش از طريق
ايجاد مثلث هاي متشابه و تصحيح آنها بعد از اضافه شدن داده جديد، كار مي
كند.
|
The Nearest Neighbor Method
The Nearest Neighbor method assigns the
value of the nearest point to each grid node. This method is useful when data
are already evenly spaced, but need to be converted to a SURFER grid file.
Alternatively, in cases where the data are close to being on a grid, with
only a few missing values, this method is effective for filling in the holes
in the data. Sometimes with nearly complete grids of data, there are areas of
missing data that you want to exclude from the grid file. In this case, you
can set the Search Ellipse to a certain value, so the areas of no data are
assigned the blanking value in the grid file. By setting the search ellipse
radii to values less than the distance between data values in your file, the
blanking value is assigned at all grid nodes where data values do not exist
Nearest Neighbor اين روش مقادير نزديكترين نقطه را به هر گره شبكه اختصاص مي دهد. کاربران قدیمی برنامه می توانند با استفاده از این روش فایل ورودی رقوم ارتفاعی زمین پروژه های قبلی خود را بدون هرگونه تغییر محسوسی به نسخه جدید منتقل و مورد استفاده و ارزیابی مجدد قرار دهند.
|
|
The Polynomial Regression Method
Polynomial Regression is used to define
large-scale trends and patterns in your data. Polynomial Regression is not
really an interpolator because it does not attempt to predict unknown Z
values. There are several options you can use to define the type of trend
surface
 Polynomial Regression اين روش براي تعريف روندها و خصوصيات بزرگ مقياس در داده ها است. |
The Radial Basis Function Interpolation Method Radial Basis Function interpolation is a diverse group of data interpolation methods. In terms of the ability to fit your data and produce a smooth surface, the multiquadric method is considered by many to be the best. All of the Radial Basis Function methods are exact interpolators, so they attempt to honor your data. You can introduce a smoothing factor to all the methods in an attempt to produce a smoother surface.  Radial Basis
Function تركيبي از روش هاي
مختلف براي توليد سطح صاف
است. |
|
The Triangulation with Linear Interpolation Method The Triangulation with Linear Interpolation method in SURFER uses the optimal Delaunay triangulation. This algorithm creates triangles by drawing lines between data points. The original points are connected in such a way that no triangle edges are intersected by other triangles. The result is a patchwork of triangular faces over the extent of the grid. This method is an exact interpolator. Each triangle defines a plane over the grid nodes lying within the triangle, with the tilt and elevation of the triangle determined by the three original data points defining the triangle. All grid nodes within a given triangle are defined by the triangular surface. Because the original data are used to define the triangles, the data are honored very closely. Triangulation with Linear Interpolation works best when your data are evenly distributed over the grid area. Data sets containing sparse areas result in distinct triangular facets on the map.
Triangulation with Linear Interpolation اين روش مثلث هاي
بهينه اي را با
وصل خطوطي بين نقاط داده ايجاد ميكند. |
|
The Moving Average Method
The Moving Average method assigns values to
grid nodes by averaging the data within the grid node's search ellipse. To
use Moving Average, a search ellipse must be defined and the minimum number
of data to use, specified. For each grid node, the neighboring data are
identified by centering the search ellipse on the node. The output grid node
value is set equal to the arithmetic average of the identified neighboring
data. If there are fewer, than the specified minimum number of data within
the neighborhood, the grid node is blanked
Moving Average اين روش مقاديري
را كه با ميانگين گيري از داده هاي داخل بيضوي نقاط شبكه بدست مي
آيد به گره هاي شبكه اختصاص مي دهد. |
The Data Metrics Methods The collection of data metrics methods creates grids of information about the data on a node-by-node basis. The data metrics methods are not, in general, weighted average interpolators of the Z-values. For example, you can obtain information such as: a) The number of data points used to interpolate each grid node. If the number of data points used is fairly equal at each grid node, then the quality of the grid at each grid node can be interpreted. b) The standard deviation, variance, coefficient of variation, and median absolute deviation of the data at each grid node. These are measures of the variability in space of the grid, which is important information for statistical analysis.
c) The distance to the nearest data point.
For example, if the XY values of a data set are sampling locations, the
Distance to the nearest data metric can be used to determine new sampling
locations. A contour map of the distance to the nearest data point can
quantify where higher sampling density may be desired
Data Metrics در اين روش واسطه يابي به صورت نقطه
به نقطه انجام مي گيرد. |
|
The Local Polynomial Method
The Local Polynomial method assigns values
to grid nodes by using a weighted least squares fit, with data within the
grid node's search ellipse
Local Polynomial در اين روش مقادير محاسبات به روش كمترين مربعات بر روي بيضوي به گره هاي شبكه اختصاص داده مي شود.
|
- نوشته شده در ۸ اردیبهشت ۱۳۹۰ |
- نظرات - ۳۳ |
- نظر بدهید
لیست کاربران:
لیست کاربران بروز رسانی شد، لازم به توضیح است که تعدادی از کاربران حقیقی مایل به انتشار مشخصات خود در سطح عموم نمی باشند و البته خواسته و حریم خصوصی ایشان برای ما محترم است.انتشارنسخه جدید:
VISUAL LEVEL 4.00
- شبیه سازی سطح سه بعدی زمین به دوازده روش حرفه ای
- نمایش سه بعدی زمین و صفحه مستوی تسطیح بطور همزمان
- رفع اشکالات گزارش شده توسط کاربران و افزایش سرعت پردازش









